1083: [NOIp2002 普及组] 过河卒
内存限制:128 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:4
解决:3
题目描述
棋盘上 $A$ 点有一个过河卒,需要走到目标 $B$ 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$,同样马的位置坐标是需要给出的。
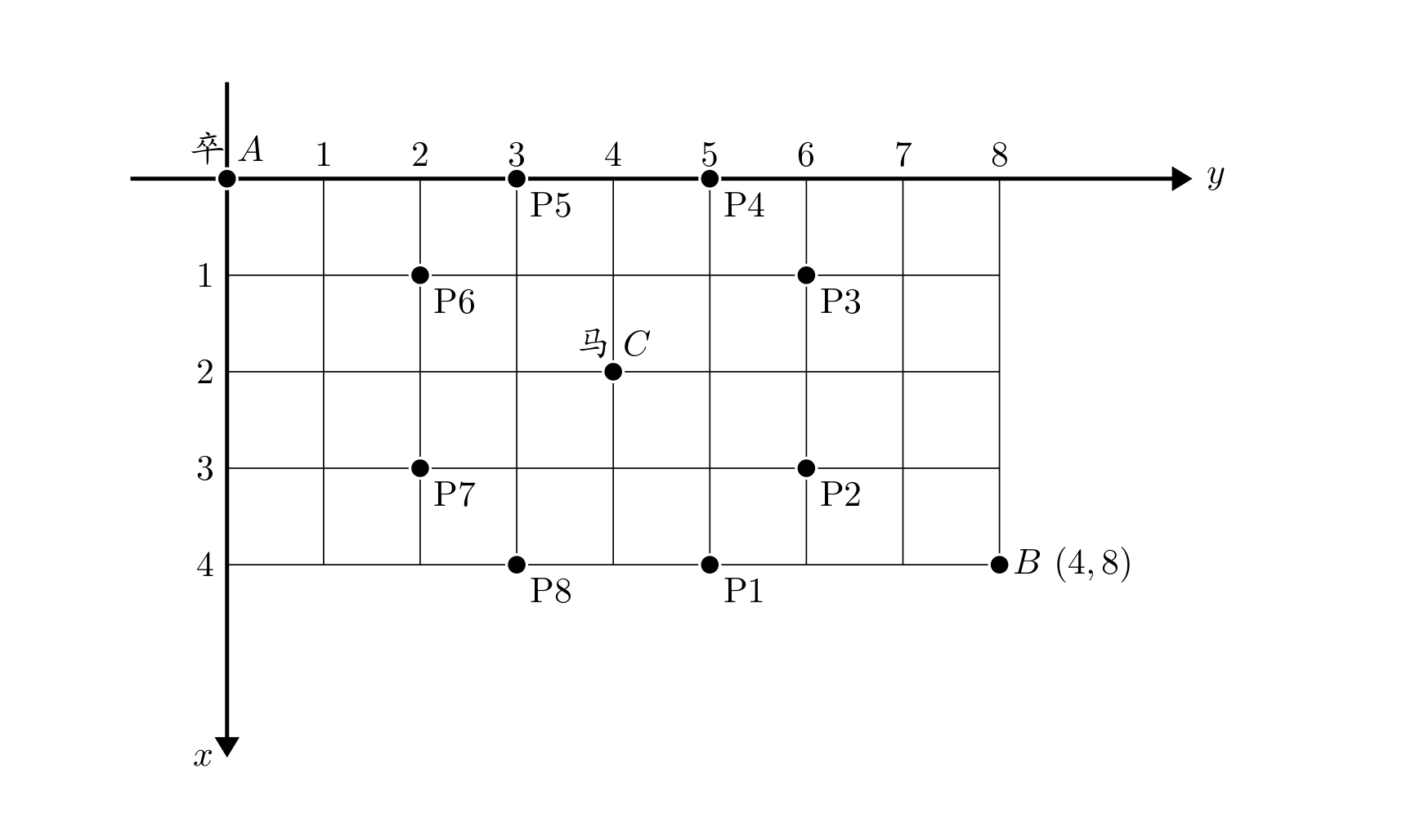
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入
一行四个正整数,分别表示 $B$ 点坐标和马的坐标。
输出
一个整数,表示所有的路径条数。
样例输入 复制
6 6 3 3样例输出 复制
6提示
**【数据范围】**
对于 $100 \%$ 的数据,$1 \leq n, m \leq 20$,$0 \leq$ 马的坐标 $\leq 20$。
NOIp2002 普及组T4